Resistor in series and parallel combinations
What will you learn?
- To find or derive the formula for equivalent resistance when resistors are in a series combination.
- How voltage gets divided among resistors connected in series.
- To find the equivalent resistance when resistors are in parallel combination.
- How current gets divided among resistors connected in parallel.
Resistors in series combination
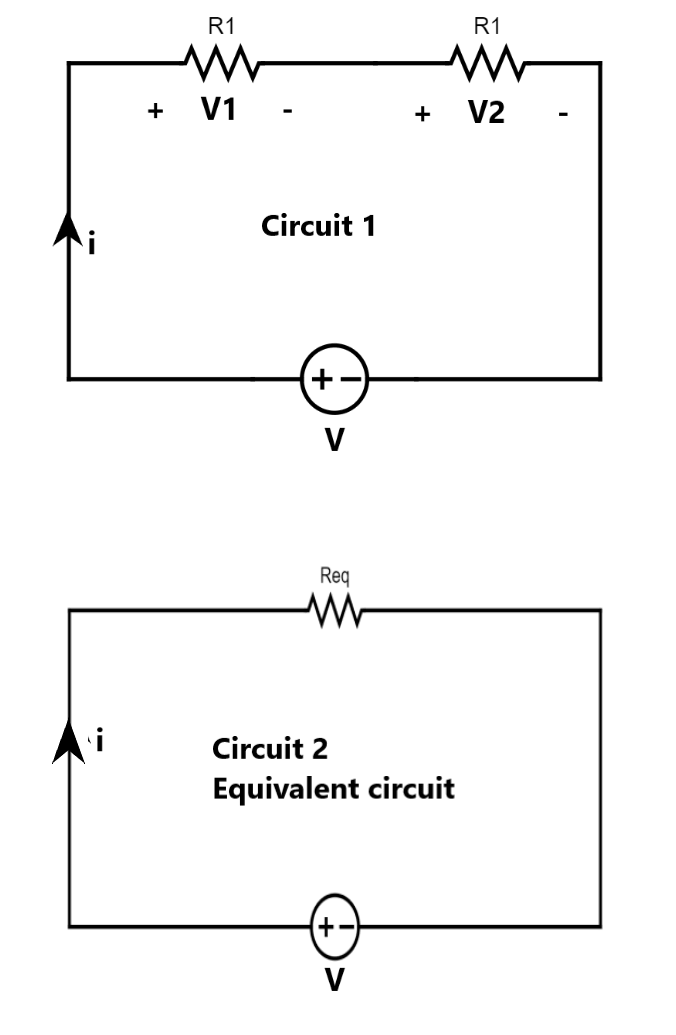
Resistors are said to be in series if they carry the same current and connected sequentially end to end. For example in the given diagram R1 and R2 are connected sequentially end to end and carry the same current. Thus we can say that R1 and R2 resistors are connected in series.
If we want to replace these two resistors with a single equivalent resistor (same v-i graph) then we have to find the value of that equivalent resistance in terms of R1 and R2.So let us find out equivalent resistance.
Applying Ohm’s law in resistors R1, R2, and Req, we have
V1=iR1 V2=iR2 [From circuit 1]
V=iReq [From circuit 2]
Now if we apply KVL law in above circuit 1, we have
V-V1-V2=0
⇒V=V1+V2
⇒iReq = iR1 + iR2 =i(R1 + R2)
⇒Req =R1 + R2
For N resistors in series
Req =R1+R2 +R3 +…..+RN-1 +RN
Resistors in a series combination behave as a single resistor (equivalent resistor) whose resistance is equal to the sum of the resistance of the individual resistor.
Voltage division rule :
If we want to find the voltage across each resistor when resistors are in series connection, then
\[V_{1}=iR_{1}= \frac{V}{R_{eq}} \times R_{1}=V \times \frac{R_{1}}{R_{eq}} \\ V_{2}=iR_{2}= \frac{V}{R_{eq}} \times R_{2}=V \times \frac{R_{2}}{R_{eq}}\\Similarly, V_{n}=V \times \frac{R_{n}}{R_{eq}} \]
If we want to find the voltage across R1 when R1 and R2 are in series connection and the voltage across both of them is V, then
\[ V_{1}=V \times \frac{R_{1}}{R_{1}+R_{2}} \]
Note: The source voltage V is divided among the resistor in direct proportion to their resistance i.e, the larger the resistance larger the voltage drop. This is called the voltage division principle.
Resistors in parallel combination
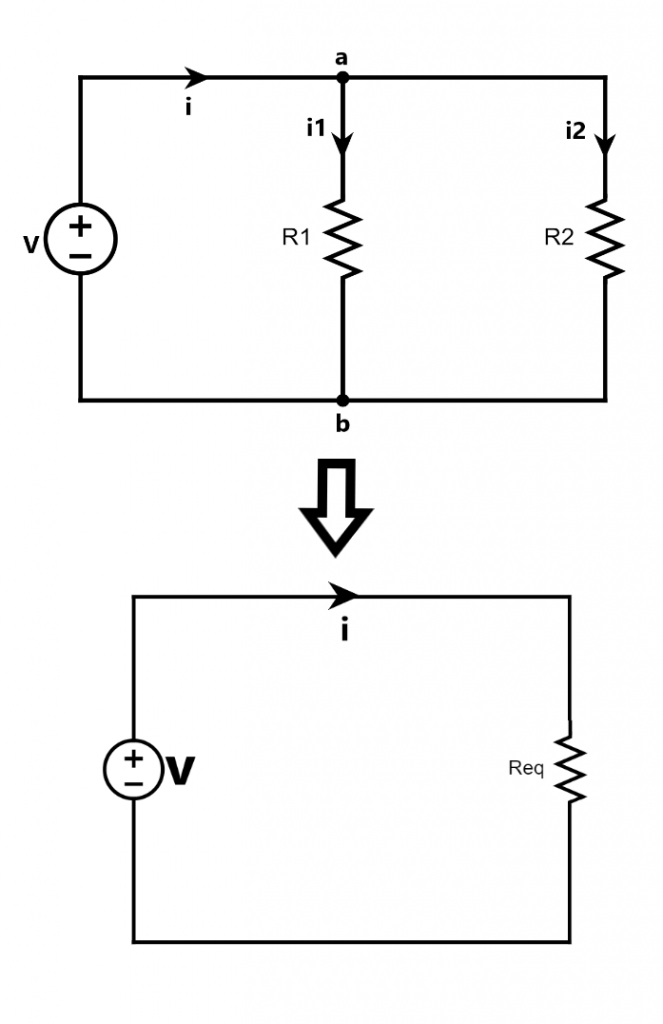
Two resistors are said to be in parallel connection if they are connected to the same nodes and consequently voltage across them is the same.
In the given figure R1 and R2 are connected between the same nodes a and b and voltage across them is also the same i.e, V.
If we want to replace these two parallel resistors with a single equivalent resistor. Then we have to find the value of equivalent resistance(Req) in terms of R1 and R2.
Applying Ohm’s law in resistors R1, R2, and Req, we have
V=i1R1 ⇒i1=V/R1
V=i2R2 ⇒i2=V/R2
V=iReq ⇒i=V/Req
Applying KCL at node a, we have
i=i1+i2
Substituting value of i1,i2 and i, we have
\[\frac{V}{R_{eq}} = \frac{V}{R_{1}} + \frac{V}{R_{2}} \\ \Rightarrow \frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}} \]
In terms of conductance(G)
Geq=G1+G2
Equivalent resistance of two resistors in parallel:
\[R_{eq}= \frac{R_{1}R_{2}}{R_{1}+R_{2}} \]
For N-resistors in parallel
\[\frac{1}{R_{eq}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}+….+\frac{1}{R_{N}}\\ if \space R_{1}=R_{2}=…..=R_{N}\\ \Rightarrow \frac{1}{R_{eq}}= \frac{N}{R} \Rightarrow R_{eq}= \frac{R}{N} \]
Notes:
- The equivalent resistance of two parallel resistors is equal to the product of their resistances divided by their sum.
- The equivalent conductance of resistors connected in parallel is the sum of their individual conductance.
- Equivalent resistance is always smaller than the resistance of the smallest resistor in parallel combination.
Current division rule
If the total current flow through node a is i and we want to find the current through resistor R1(i1)and R2(i2), then
\[i_{1}= \frac{V}{R_{1}} = \frac{iR_{eq}}{R_{1}} = \frac{i \frac{R_{1}R_{2}}{R_{1}+R_{2}} }{ R_{1}} \\ \Rightarrow i_{1}=i \times \frac{R_{2}}{R_{1}+R_{2}}\space ……(1) \\Similarly, i_{2}=i \times \frac{R_{1}}{R_{1}+R_{2}}\space ……(2)\]
This shows that the total current i shared is shared by the resistors in inverse proportion to their resistances. That is larger the resistance of a resistor smaller the part of total current flow through it. This is known as the current division rule.
Consider an electric circuit consists of two resistors R1 and R2 connected in parallel and the total current flow through them is ‘i’. Now take two extreme value for resistance of R2 and see what happened:
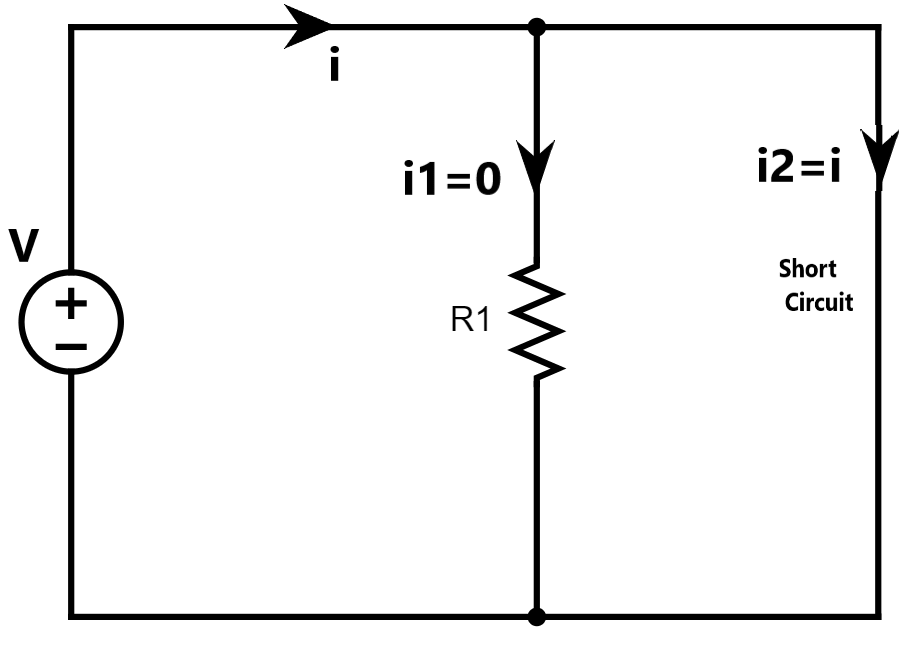
Case1: If R2 =0 {Short Circuit}
By putting R2 =0 in above equation (1) ,we get i1 =0 this implies that i2=i. That means that the entire current i bypasses R1 and flows through the circuit R2 =0, the path of least resistance. Thus when a circuit is short-circuited as shown in the figure, these points to be kept in mind:
- The equivalent resistance Req=0.
- The entire current flows through the circuit.
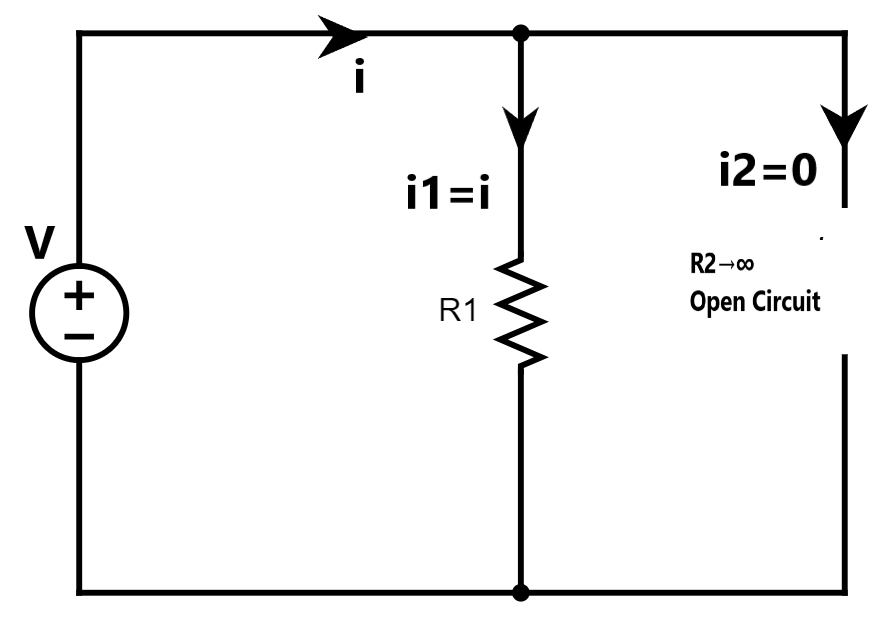
Case 2: If R2=∞ {Open Circuit}
Current i will flow through path R1 because R2 behaves as an open circuit. And equivalent resistance Req=R1[By taking limit R2→∞ in the equation of equivalent resistance]